Low-Code Programming for Knowledge Reasoning
| Id | Status | Submission Date | Publish Date | Authorship |
|---|---|---|---|---|
| US18/078,566 | Pending | 12 Sep 2022 | 13 Jun 2024 | 100% |
Business processes are typically encoded in software through several phases: functional analysis, architectural design, software implementation, and quality checking. Each phase involves distinct roles and expertise. When small teams with limited technical skills need to implement a simple workflow or update an existing one, they often rely on external developers, leading to increased costs and delays.

To address this and promote independence from technical constraints, a programming system should:
- Integrate diverse data sources across types and domains.
- Focus on logical/business data manipulation without concern for formats and protocols.
- Enable easy solutions for simple problems while allowing complex problems to be solvable.
- Support reuse of existing functionalities.
- Handle complex computations, such as recursion.
- Centralize all business logic in a single repository, separate from integration systems/configurations.
- Provide online program editing and REST API queries in a serverless environment.
Many low-code/no-code platforms fail to meet these needs, as they are either too rigid for customization or unsuitable for anything beyond basic use cases (e.g., mobile app builders).
SUPPLY CHAIN USE CASE
Consider a simple example: we work for an international manufacturing company with branches worldwide. Complex products like cars are made up of numerous components, many of which are further broken down into subparts produced by other branches or suppliers. As part of the supply management team, our task is to generate reports on production costs throughout the supply chain. One such product is the ‘i3’ electric car, which includes—among other components—a battery manufactured in China using materials sourced from Chile, as shown here:
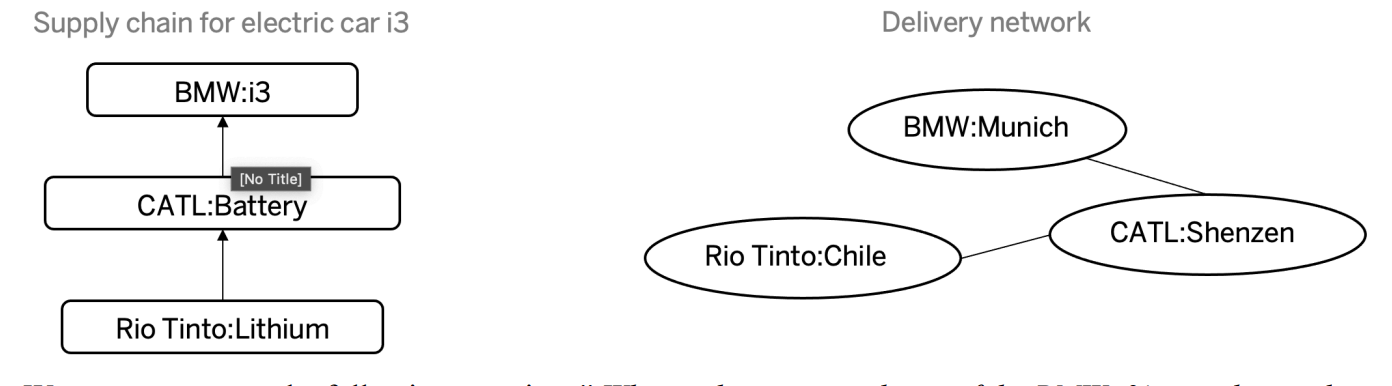
We want to answer the question: “What is the compound cost of the BMW i3’s supplies and their delivery to Munich?”
Answering this requires computation, especially when the data isn’t structured specifically for the query. Let’s create a hypothetical database to store information about locations, producers, products, their parts, and associated costs (including delivery costs). We’ll use a logical abstraction where data (facts) is represented as tuples, with the first argument indicating the relation and the remaining arguments defining its elements. For example:
("locatedAt", "bmw", "Munich") means BMW is located in Munich.
("produces", "bmw", "i3", 20000) means BMW produces the i3 at a cost of 20,000.
("deliveryCost", "Chile", "Shenzhen", 100) means the delivery cost from Chile to Shenzhen is 100.
Facts in the Database
("locatedAt", "bmw", "Munich")
("locatedAt", "catl", "Shenzhen")
("locatedAt", "rio", "Chile")
("produces", "bmw", "i3", 20000)
("produces", "catl", "battery pack", 5000)
("produces", "rio", "lithium", 1000)
("partOf", "battery pack", "i3")
("partOf", "lithium", "battery pack")
("deliveryCost", "Chile", "Shenzhen", 100)
("deliveryCost", "Shenzhen", "Munich", 90)
Defining the program
The program structure mirrors the data and uses tuples with variables (propositional logic). Variables are strongly typed with four primitive types: string, int, double, and boolean. For example, item and consumer are Var[String], while deliveryCost is Var[Int].
To calculate delivery costs:
("costDelivery", item, consumer, deliveryCost) :- (("produces", supplier, item, xi),
("locatedAt", consumer, loc1),
("locatedAt", supplier, loc2),
("deliveryCost", loc2, loc1, deliveryCost))
The cost of non-composed items is simply the producer’s price:
("costItem", item, cost) :- (("produces", partner, item, cost),
not(("partOf", item2, item)))
To check if an item isn’t composed, we ensure no fact exists that defines it as part of another:
not(("partOf", item2, item))
For composed items, the total cost includes the item’s price, the cost of its components, and delivery:
("costItem", item, costTot) :- (("produces", partner, item, cost),
("partOf", item2, item),
("costDelivery", item2, partner, deliveryCost),
("costItem", item2, cost2), // recursive call
costTot := cost + cost2 + deliveryCost)
The system uses recursion for elegance and simplicity. The base case is the non-composed item cost.
Querying the program
We can query the system using the same tuple format:
?("costItem", item, cost)
Example result:
+--------------+-------+-------+
| Item | Cost | Check |
+--------------+-------+-------+
| battery pack | 6100 | true |
| i3 | 26190 | true |
| lithium | 1000 | true |
+--------------+-------+-------+
Here, the check variable indicates if the row exists. For example, querying an undefined item like “Ferrari” returns:
+---------+------+-------+
| Item | Cost | Check |
+---------+------+-------+
| Ferrari | | false |
+---------+------+-------+
This shows no program or data satisfies the request, so the check variable is false.
Programming Experience (PX)
Users can interact with the system through two primary channels: on-premise and cloud solutions.
- On-Premise Solution: This traditional approach involves building software artifacts by writing programs in a programming language, compiling, assembling, and deploying them to an application server. In this setup, the system is used within a programming environment (e.g., Scala), leveraging intrinsic compilation capabilities for error checking and validation during development.
- Cloud-Based Online Development: Users can develop programs via a dedicated web-based tool, enabling real-time editing, testing, and automated deployment through a development pipeline. Once approved, the programs are deployed and made accessible via REST APIs, allowing integration with external applications or web frontends.
Simplified PX
The system offers an intuitive and efficient programming experience, characterized by the following features:
- Declarative and Concise Language: Focus solely on business logic, eliminating unnecessary syntax and boilerplate code.
- Composition and Reusability: Functions and predicates can call one another, enabling modularization and reuse across different programs.
- Semantic Algebra: Variables facilitate intuitive joins and data manipulation within predicates.
- Mathematical Directives: Built-in support for common mathematical operations, aggregations, and filtering.
- Serverless Architecture: Programs can be created, tested, and served online through web services without the need for infrastructure management.
Data structure
Internally, data is stored as column-oriented dense matrices, a structure also used for input and output in clauses. A matrix consists of a vector of columns, where each column represents a specific variable’s values. In a column-oriented design, data is stored contiguously by column rather than by row. To retrieve a row at position i, values from all columns at position i must be collected.
Columns are rectangular, meaning they all have the same length, corresponding to the total number of rows. While this column-based structure optimizes operations like renaming matrices across different predicates, it comes at the cost of less efficient row-based operations.
Variables are managed in a separate field (vars), which maps each variable to its corresponding column and position. Additionally, a control variable (checks) tracks the validity of rows. This is implemented as a boolean vector, where true indicates that the row at position i (checks(i)) is valid, and false marks it as invalid.
Proposition disjunction (OR/SUM)
In the supply chain example, the (costItem, string, int) predicate is declared twice: once for non-composite items and once for composed items, reflecting recursion. While the semantic distinction makes sense, handling multiple predicate definitions must be managed independently of their semantics. The system treats predicates of the same type as a logical disjunction (OR), meaning the results are combined like a sum.
Example: Consider two matrices a and b with the same type (Var[Int], Var[Int], Var[Int]) from two head clauses. These matrices are merged via the OR operation:
Matrix a
|x | y| z|check|
|--|---|----|-----|
|2 | 20| 200| true|
|1 | 10| 100| true|
Matrix b
|x | y| z|check|
|--|---|----|-----|
|1 | 10| 100|false|
|2 | 20| 200| true|
The OR operation merges non-conflicting rows—rows where values match or one of them is null. The check column will be true if either a or b is true, otherwise, it will be false.
Resulting OR merge (a OR b):
|x | y| z|check|
|--|---|----|-----|
|1 | 10| 100|false|
|2 | 20| 200| true|
This result corresponds to the following program:
(‘a’,1,10,100)
(‘a’,2,20,200)
(‘b’,2,20,200)
(‘p’,x,y,z) :- (‘a’,x,y,z)
(‘p’,x,y,z) :- (‘b’,x,y,z)
?(‘p’,x,y,z)
Proposition conjunction (AND/product)
The body elements, separated by commas, represent a conjunction (AND operation), which can be interpreted as either joining results or filtering existing data.
For example:
(("produces", partner, item, cost),
not(("partOf", item2, item)))
This body consists of two predicates, connected by a variable, and the resulting values satisfy both conditions: one for the produces relationship, and the other for items that are not composed of parts.
Body elements can also represent new variable instantiations. For instance:
costTot := cost + cost2 + deliveryCost
In this case, costTot is logically associated with cost, cost2, and deliveryCost, and its value is the sum of these components.
Furthermore, explicit filtering can be applied:
costTot := cost + cost2 + deliveryCost, costTot > 1000
This ensures that only results with a costTot greater than 1000 are returned.
Thus, body elements separated by commas are logically connected with conjunctions (AND), meaning all conditions must be satisfied for a result to be returned. The conjunction of predicates results in data filtering if the predicates’ signatures do not introduce new variables. It results in joins when the intersection and disjunction of variables are both non-empty (e.g., data a with variables x, y, and data b with variables y, z).
Example with Filtering:
Matrix a:
|x | y|check|
|--|--|-----|
|1 |10|true |
|2 |20|true |
|3 |30|true |
Matrix b:
|x | y|check|
|--|--|-----|
|1 |10|true |
|2 |20|true |
|3 |30|false|
Result of a AND b:
|x | y|check|
|--|--|-----|
|1 |10|true |
|2 |20|true |
In this example, the row (x=1, y=10) remains unchanged, while the row (x=2, y=20, check=true) is merged from both matrices, with the values from matrix a retained. The third row (x=3, y=30) is filtered out because its check value is false in matrix b.
This behavior corresponds to the following program:
(‘a’,1,10)
(‘a’,2,20)
(‘a’,3,30)
(‘b’,1,10)
(‘b’,2,20)
(‘p’,x,y) :- (‘a’,x,y), (‘b’,x,y)
?(‘p’,x,y)
Data sources
The data used in the supply chain example is primarily for demonstration and prototyping, not for real-world adoption. In practical applications, data should be fetched from external sources through proper configuration, taking advantage of the high abstraction between data and programs.
Given the graph-based nature of predicate representation, graph databases are the most intuitive choice for interfacing with data sources. Predicates can be easily mapped to SPARQL queries, as the data is structured as relationships between nodes. With appropriate configuration, specific relations in the program can be linked to corresponding external database relations. For example, the supply chain data tuples can be retrieved from graph, relational, or key-value store databases.
The internal database used in the prototype relies on general algorithms for performing logical disjunctions and conjunctions to query the required data.